1091. Shortest Path in Binary Matrix

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

• All the visited cells of the path are 0.
• All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

Example 1:

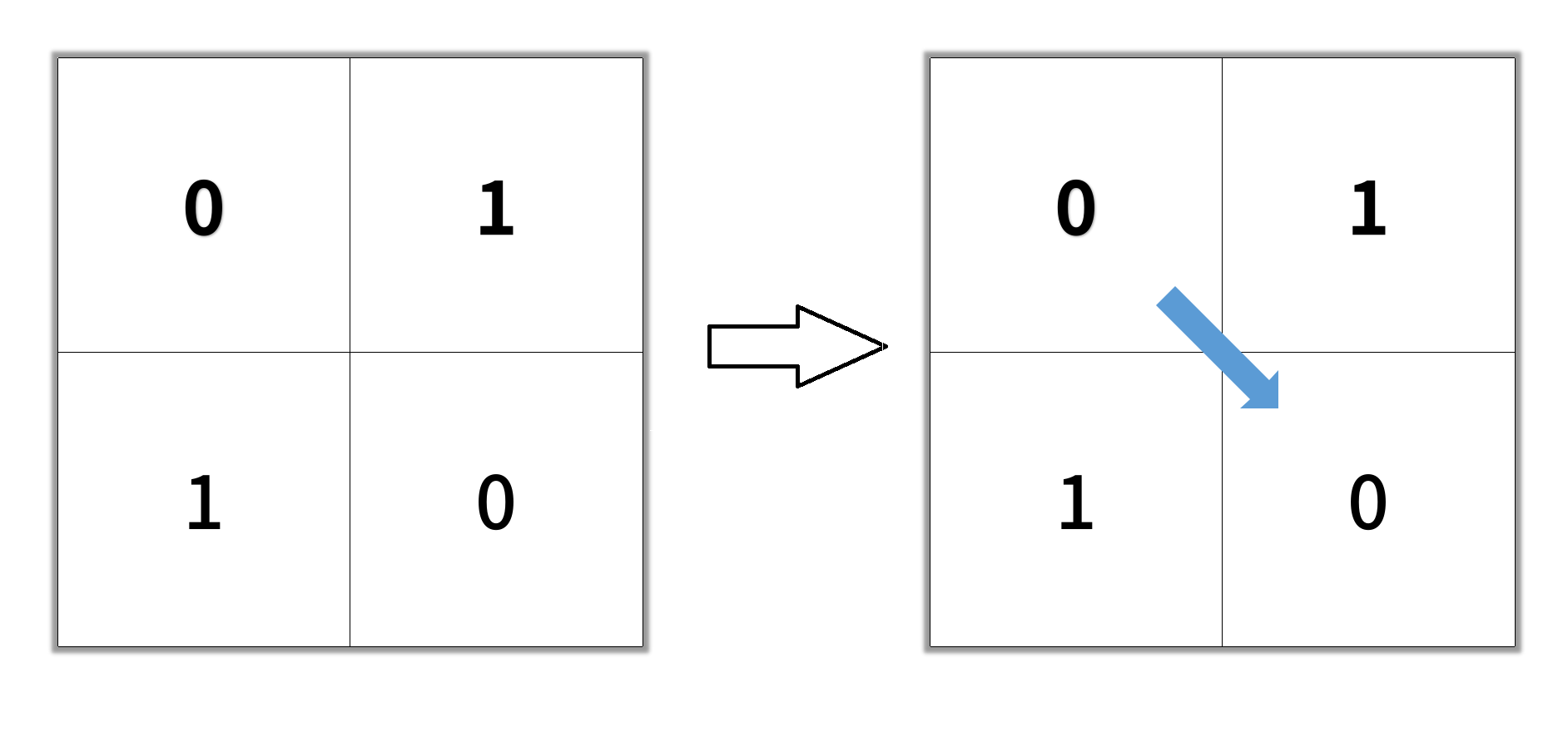
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

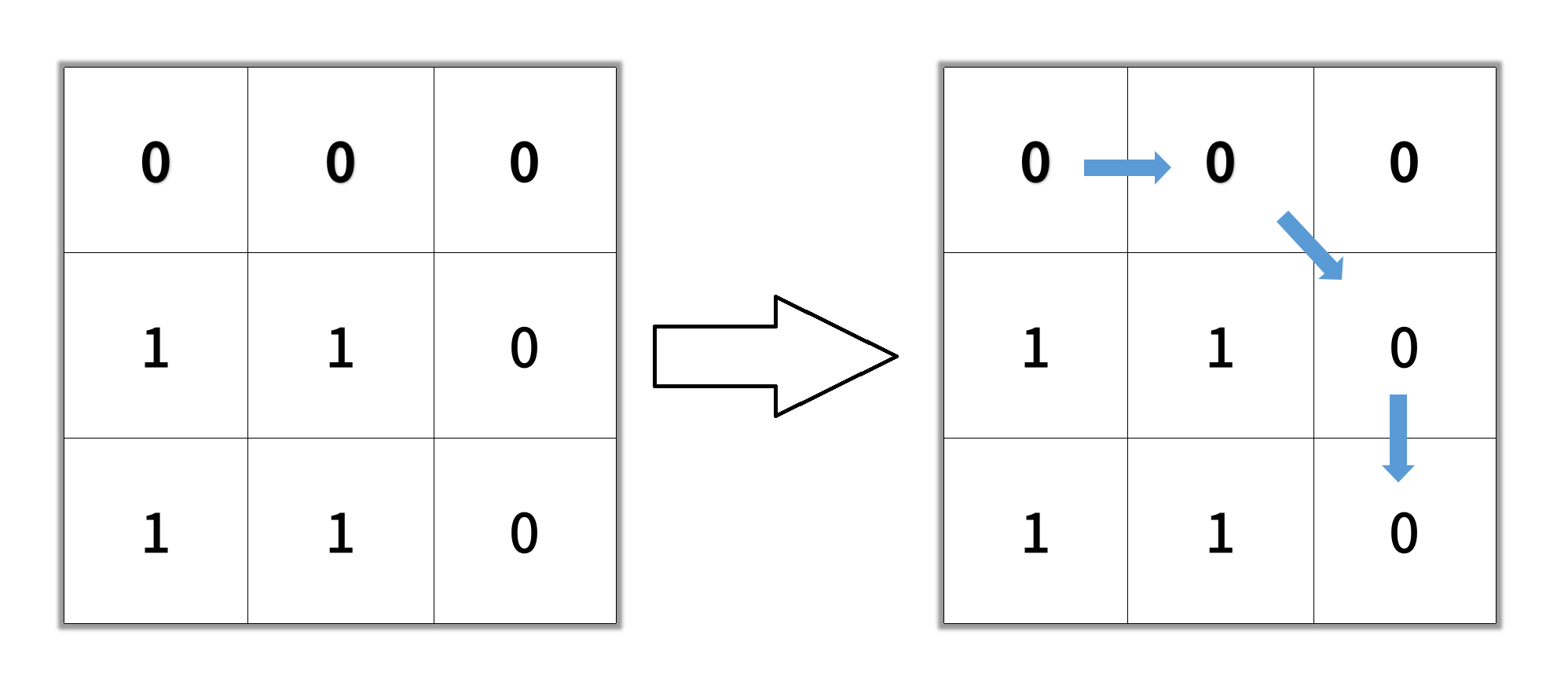
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] is 0 or 1

Solutions (Rust)

1. BFS

use std::collections::HashSet;
use std::collections::VecDeque;

impl Solution {
    pub fn shortest_path_binary_matrix(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let mut seen = vec![(0, 0)].into_iter().collect::<HashSet<_>>();
        let mut cells = vec![(0, 0, 1)].into_iter().collect::<VecDeque<_>>();

        if grid[0][0] == 1 || grid[n - 1][n - 1] == 1 {
            return -1;
        }

        while let Some((x, y, length)) = cells.pop_front() {
            if x == n - 1 && y == n - 1 {
                return length;
            }
            for x_ in x.saturating_sub(1)..(x + 2).min(n) {
                for y_ in y.saturating_sub(1)..(y + 2).min(n) {
                    if grid[x_][y_] == 0 && !seen.contains(&(x_, y_)) {
                        seen.insert((x_, y_));
                        cells.push_back((x_, y_, length + 1));
                    }
                }
            }
        }

        -1
    }
}