Segment Trees

In Computer science, a segment tree is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, it's a structure that cannot be modified once it's built. A similar data structure is the interval tree.
In Computer science, a segment tree is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, it's a structure that cannot be modified once it's built. A similar data structure is the interval tree.A segment tree for a set I of n intervals uses O(n log n) storage and can be built in O(n log n) time. Segment trees support searching for all the intervals that contain a query point in O(log n + k), k being the number of retrieved intervals or segments.[1] Applications of the segment tree are in the areas of computational geometry, and geographic information systems. The segment tree can be generalized to higher dimension spaces as well.
~~https://en.wikipedia.org/wiki/File:Segment_tree.svg~~
SEGMENT TREES DESCRIPTION Given a set I of intervals, or segments, a segment tree T for I is structured as follows: T is a binary tree. Its leaves correspond to the elementary intervals induced by the endpoints in I, in an ordered way: the leftmost leaf corresponds to the leftmost interval, and so on. The elementary interval corresponding to a leaf v is denoted Int(v). The internal nodes of T correspond to intervals that are the union of elementary intervals: the interval Int(N) corresponding to node N is the union of the intervals corresponding to the leaves of the tree rooted at N. That implies that Int(N) is the union of the intervals of its two children. Each node or leaf v in T stores the interval Int(v) and a set of intervals, in some data structure. This canonical subset of node v contains the intervals [x, x′] from I such that [x, x′] contains Int(v) and does not contain Int(parent(v)). That is, each node in T stores the segments that span through its interval, but do not span through the interval of its parent.
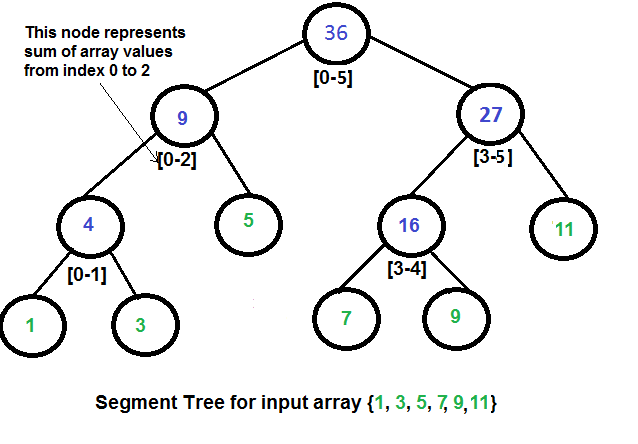
Below is a example of segment tree:
SEGMENT TREES DESCRIPTION

Given a set I of intervals, or segments, a segment tree T for I is structured as follows: T is a binary tree. Its leaves correspond to the elementary intervals induced by the endpoints in I, in an ordered way: the leftmost leaf corresponds to the leftmost interval, and so on. The elementary interval corresponding to a leaf v is denoted Int(v).
The internal nodes of T correspond to intervals that are the union of elementary intervals: the interval Int(N) corresponding to node N is the union of the intervals corresponding to the leaves of the tree rooted at N. That implies that Int(N) is the union of the intervals of its two children.
Each node or leaf v in T stores the interval Int(v) and a set of intervals, in some data structure. This canonical subset of node v contains the intervals [x, x′] from I such that [x, x′] contains Int(v) and does not contain Int(parent(v)). That is, each node in T stores the segments that span through its interval, but do not span through the interval of its parent.
Construction of Segment trees

~~Construction of Segment trees~~ This section describes the construction of a segment tree in a one-dimensional space. A segment tree from the set of segments I, can be built as follows. First, the endpoints of the intervals in I are sorted. The elementary intervals are obtained from that. Then, a balanced binary tree is built on the elementary intervals, and for each node v it is determined the interval Int(v) it represents. It remains to compute the canonical subsets for the nodes. To achieve this, the intervals in I are inserted one by one into the segment tree. An interval X = [x, x′] can be inserted in a subtree rooted at T, using the following procedure:[5] If Int(T) is contained in X then store X at T, and finish. Else: If X intersects the interval of the left child of T, then insert X in that child, recursively. If X intersects the interval of the right child of T, then insert X in that child, recursively. The complete construction operation takes O(nlogn) time, n being the number of segments in I.:
Query This section describes the query operation of a segment tree in a one-dimensional space. A query for a segment tree, receives a point qx(should be one of the leaves of tree), and retrieves a list of all the segments stored which contain the point qx. Formally stated; given a node (subtree) v and a query point qx, the query can be done using the following algorithm: Report all the intervals in I(v). If v is not a leaf: If qx is in Int(left child of v) then Perform a query in the left child of v. If qx is in Int(right child of v) then Perform a query in the right child of v. In a segment tree that contains n intervals, those containing a given query point can be reported in O(logn + k) time, where k is the number of reported intervals.
If Int(T) is contained in X then store X at T, and finish. Else:
If X intersects the interval of the left child of T, then insert X in that child, recursively.
If X intersects the interval of the right child of T, then insert X in that child, recursively. The complete construction operation takes O(nlogn) time, n being the number of segments in I.
Query

This section describes the query operation of a segment tree in a one-dimensional space. A query for a segment tree, receives a point qx(should be one of the leaves of tree), and retrieves a list of all the segments stored which contain the point qx. Formally stated; given a node (subtree) v and a query point qx, the query can be done using the following algorithm:
Report all the intervals in I(v).
If v is not a leaf:
If qx is in Int(left child of v) then Perform a query in the left child of v.
If qx is in Int(right child of v) then Perform a query in the right child of v.
In a segment tree that contains n intervals, those containing a given query point can be reported in O(logn + k) time, where k is the number of reported intervals.