Recursão é uma técnica usada em ciência da computação para resolver grandes problemas, dividindo-os em problemas menores e similares. O processo no qual uma função chama a si mesma direta ou indiretamente é chamado de recursão e a função correspondente é chamada de função recursiva. Usando um algoritmo recursivo, certos problemas podem ser resolvidos facilmente.
O processo no qual uma função chama a si mesma direta ou indiretamente é chamado de recursão e a função correspondente é chamada de função recursiva.
- Um algoritmo recursivo dá um passo em direção à solução e então recursivamente chama a si mesmo para mover-se mais. O algoritmo para quando alcançamos a solução.
- Como a função chamada pode chamar a si mesma, esse processo pode continuar para sempre. Então é essencial fornecer um caso base para terminar esse processo de recursão.
- A recursão ajuda na construção lógica. O pensamento recursivo ajuda a resolver problemas complexos ao dividi-los em subproblemas menores.
- Soluções recursivas funcionam como base para algoritmos de Programação Dinâmica e Divisão para Conquista.
- Certos problemas podem ser resolvidos facilmente usando recursão, como
Torres de Hanói (TOH),Travessias de Árvores Inorder/Preorder/Posorder,DFS de Grafos, etc.
-
Etapa 1 – Defina um caso base: Identifique o caso mais simples (ou base) para o qual a solução é conhecida ou trivial. Esta é a condição de parada para a recursão, pois impede que a função se chame infinitamente.
-
Etapa 2 – Defina um caso recursivo: Defina o problema em termos de subproblemas menores. Divida o problema em versões menores de si mesmo e chame a função recursivamente para resolver cada subproblema.
-
Etapa 3 – Garanta que a recursão termine: Certifique-se de que a função recursiva eventualmente alcance o caso base e não entre em um loop infinito.
-
Etapa 4 – Combine as soluções: Combine as soluções dos subproblemas para resolver o problema original.
Vamos considerar um problema para encontrar a soma de números naturais, há várias maneiras de fazer isso, mas a abordagem mais simples é simplesmente adicionar os números começando de 0 a n. Então a função simplesmente se parece com isso, abordagem(1) - Simplesmente adicionando um por um
f(n) = 0 + 1 + 2 + 3...+ n
mas há outra abordagem matemática para representar isso, abordagem(2) – Adição recursiva
f(n) = 0 n=0
f(n) = n + f(n-1) n>=1
// Recursive function to find the sum of
// numbers from 0 to n
public class GfG{
public static int findSum(int n) {
// Base case
if (n == 0)
return 0;
// Recursive case
return n + findSum(n - 1);
}
public static void main(String[] args) {
int n = 5;
System.out.println(findSum(n));
}
}OUTUPT: 15
- Qual é a condição base na recursão? Um programa recursivo para em uma condição base. Pode haver mais de uma condição base em uma recursão. No programa acima, a condição base é quando n = 1.\
- Como um problema específico é resolvido usando recursão? A ideia é representar um problema em termos de um ou mais problemas menores, e adicionar uma ou mais condições base que parem a recursão.
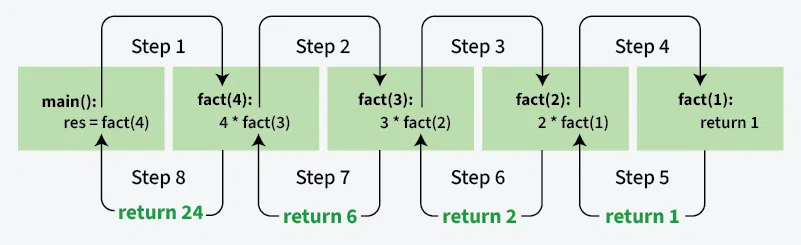
O fatorial de um número n (onde n >= 0) é definido como multiplicação de números de 1 a n. Para computação recursiva, calculamos o fatorial n se soubermos o fatorial de (n-1). O caso base para fatorial seria n = 0. Retornamos 1 quando n = 0.
public class GfG {
public static int fact(int n) {
// BASE CONDITION
if (n == 0)
return 1;
return n * fact(n - 1);
}
public static void main(String[] args) {
System.out.println("Factorial of 5 : " + fact(5));
}
}OUTUPT: Factorial of 5 : 120
Quando ocorre o erro Stack Overflow na recursão? Se o caso base não for alcançado ou não for definido, então o problema de stack overflow pode surgir. Vamos dar um exemplo para entender isso.
int fact(int n)
{
// caso base errado (pode causar
// estouro de pilha).
if (n == 100)
return 1;
else
return n*fact(n-1);
}Se fact(10) for chamado, ele chamará fact(9), fact(8), fact(7), e assim por diante, mas o número nunca chegará a 100. Então, o caso base não é alcançado. Se a memória for esgotada por essas funções na pilha, isso causará um erro de estouro de pilha.
Qual é a diferença entre recursão direta e indireta? Na recursão direta A função chama a si mesma diretamente (exemplo do cálculo do fatorial). Já na
recursão indireta uma função chama outra, e essa outra função chama a função original. Aqui está um exemplo usando duas funções A e B, onde ambas se chamam mutuamente.
Exemplo de Recursão Direta:
public class RecursaoDireta {
// Função para calcular o fatorial de um número
public static int fatorial(int n) {
if (n == 0) {
return 1; // Caso base: fatorial de 0 é 1
} else {
return n * fatorial(n - 1); // Chamada recursiva
}
}
public static void main(String[] args) {
int numero = 5;
System.out.println("Fatorial de " + numero + " é: " + fatorial(numero));
}
}Neste exemplo, a função fatorial chama a si mesma diretamente até atingir o caso base (n == 0).
Exemplo de Recursão Indireta:
public class RecursaoIndireta {
// Função A chama a função B
public static int A(int n) {
if (n <= 0) {
return 1; // Caso base
} else {
return n * B(n - 1); // Chamada para a função B
}
}
// Função B chama a função A
public static int B(int n) {
if (n <= 0) {
return 1; // Caso base
} else {
return n * A(n - 1); // Chamada para a função A
}
}
public static void main(String[] args) {
int numero = 5;
System.out.println("Resultado de A(" + numero + ") é: " + A(numero));
}
}Neste exemplo, a função A chama a função B, e a função B chama novamente a função A, formando uma recursão indireta entre ambas as funções. Esse exemplo é simples, mas a recursão indireta pode se tornar mais complexa dependendo de como as funções se interagem.
A diferença entre recursão com cauda e recursão sem cauda está na posição da chamada recursiva dentro da função e na maneira como o compilador ou interpretador pode otimizar essa recursão.
A recursão com cauda ocorre quando a chamada recursiva é a última operação realizada pela função antes de retornar o resultado. Nesse caso, o compilador pode otimizar a recursão, transformando-a em um loop (um processo chamado de tail call optimization). Essa otimização evita que a pilha de chamadas cresça, prevenindo o estouro de pilha, o que é uma limitação comum em recursões tradicionais.
public class RecursaoComCauda {
// Função que realiza a soma dos números de 1 a n usando recursão com cauda
public static int soma(int n, int acumulador) {
if (n <= 0) {
return acumulador;
} else {
return soma(n - 1, acumulador + n); // Chamada recursiva na cauda
}
}
public static void main(String[] args) {
int resultado = soma(5, 0); // Começa a soma com acumulador igual a 0
System.out.println("Resultado da soma: " + resultado);
}
}No exemplo acima, a função soma tem a chamada recursiva soma(n - 1, acumulador + n) na cauda. O valor acumulado é passado como argumento, e a operação é realizada antes da chamada recursiva, permitindo uma otimização.
A recursão sem cauda ocorre quando a chamada recursiva não é a última operação antes de retornar o valor. Normalmente, isso exige que o sistema mantenha as informações de cada chamada recursiva na pilha até que a função termine completamente, o que pode levar ao estouro de pilha em casos de recursões profundas.
public class RecursaoSemCauda {
// Função que realiza a soma dos números de 1 a n usando recursão sem cauda
public static int soma(int n) {
if (n <= 0) {
return 0;
} else {
return n + soma(n - 1); // Chamada recursiva sem cauda
}
}
public static void main(String[] args) {
int resultado = soma(5); // Chama a função com n = 5
System.out.println("Resultado da soma: " + resultado);
}
}Neste exemplo, a chamada recursiva soma(n - 1) não é a última operação a ser realizada. Após retornar de soma(n - 1), o valor de n precisa ser somado ao resultado da chamada recursiva. Isso significa que a pilha de chamadas precisa ser mantida até que todas as chamadas recursivas terminem.
- Recursão com cauda: A chamada recursiva é a última operação antes de retornar, permitindo que o compilador otimize a recursão (geralmente com tail call optimization), evitando o crescimento da pilha.
- Recursão sem cauda: A chamada recursiva não é a última operação, o que exige o armazenamento do estado da função em cada chamada recursiva. Isso pode resultar em um uso maior da pilha e levar a um estouro de pilha em casos de recursões profundas.
Em Java, a linguagem não faz otimização automática de recursão com cauda (tail call optimization), então ambas as abordagens podem levar ao estouro de pilha se o número de recursões for grande. A recursão com cauda é, portanto, mais eficiente se a linguagem oferecer suporte para otimizações desse tipo.