README.md

Algoritmos de ordenação são usados para organizar uma lista de elementos em uma ordem específica, como crescente ou decrescente , ou qualquer outra ordem especificada pelo usuário, como classificação de strings por comprimento.

Por que os algoritmos de Ordenação são Importantes?

O algoritmo de ordenação é importante na Ciência da Computação porque reduz a complexidade de um problema. Há uma ampla gama de aplicações para esses algoritmos, incluindo algoritmos de busca, algoritmos de banco de dados, métodos de dividir e conquistar e algoritmos de estrutura de dados.

Nas seções a seguir, listamos algumas aplicações científicas importantes onde algoritmos de classificação são usados

• Quando você tem centenas de conjuntos de dados que deseja imprimir, talvez seja necessário organizá-los de alguma forma.
• Depois de classificar os dados, podemos obter o k-ésimo menor e o k-ésimo maior item em tempo O(1).
• Pesquisar qualquer elemento em um enorme conjunto de dados se torna fácil. Podemos usar o método de pesquisa Binary para pesquisar se tivermos dados classificados. Então, a classificação se torna importante aqui.
• Eles podem ser usados em software e em problemas conceituais para resolver problemas mais avançados.

Noções Básicas de Ordenação

• Classificação no Local: Um algoritmo de classificação no local usa espaço constante para produzir a saída ( modifica apenas a matriz fornecida). Exemplos: classificação por seleção, classificação por bolha, classificação por inserção e classificação por heap.
• Classificação Interna: Classificação Interna é quando todos os dados são colocados na memória principal ou na memória interna . Na classificação interna, o problema não pode receber entrada além do tamanho da memória alocada.
• Classificação Externa: classificação externa é quando todos os dados que precisam ser classificados não precisam ser colocados na memória de uma vez, a classificação é chamada de classificação externa. A classificação externa é usada para uma quantidade enorme de dados. Por exemplo, a classificação por mesclagem pode ser usada na classificação externa, pois o array inteiro não precisa estar presente o tempo todo na memória,
• Classificação Estável: quando dois itens iguais aparecem na mesma ordem em dados classificados como no array original, chamado de classificação estável. Exemplos: Merge Sort, Insertion Sort, Bubble Sort.
• Classificação Híbrida: Um algoritmo de classificação é chamado Híbrido se ele usa mais de um algoritmo de classificação padrão para classificar o array. A ideia é aproveitar as vantagens de vários algoritmos de classificação. Por exemplo, o IntroSort usa Insertions sort e Quick Sort.

Tipos de Técnicas de Ordenação

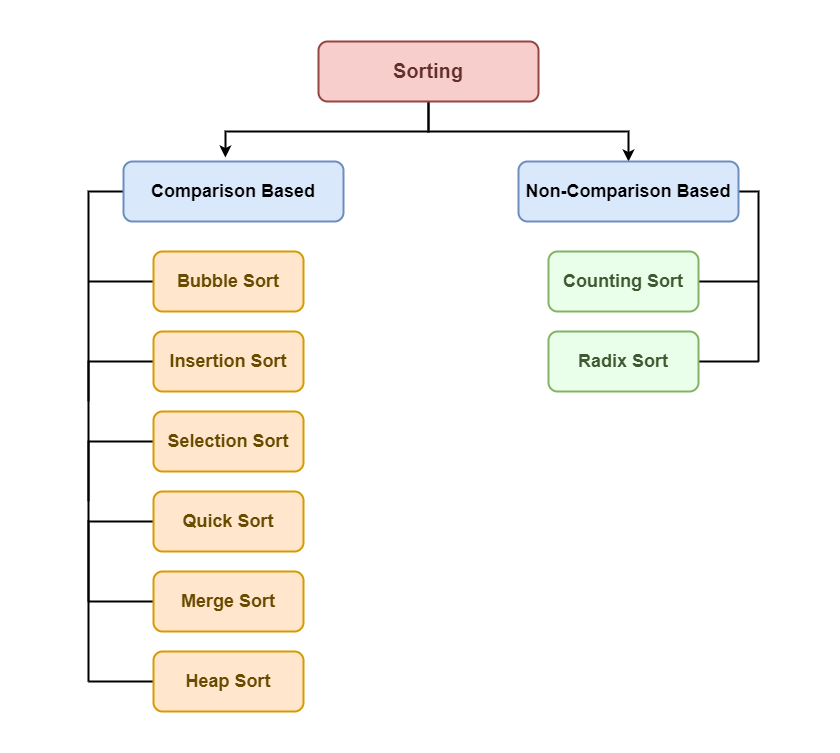
Existem vários algoritmos de ordenação usados em estruturas de dados. Os dois tipos de algoritmos de ordenação a seguir podem ser amplamente classificados:

1. Algoritmos que precisam realizar comparações entre os elementos dentro de um array ou matriz para efetuar a ordenação, são eles: Bubble Sort, Insertion Sort, Selection Sort, Quick Sort, Merge Sort e Heap Sort.
2. Algoritmos que não precisam realizar comparações entre os elementos dentro de um array ou matriz para efetuar a ordenação, são eles: Counting Sort e Radix Sort.

Aplicações de Algoritmos de Ordenações:

• Encontrando rapidamente o k-ésimo menor ou o k-ésimo maior: Depois de classificar a matriz, podemos encontrar o k-ésimo menor e o k-ésimo maior elemento em tempo O(1) para diferentes valores de k.
• Algoritmos de pesquisa: a classificação geralmente é uma etapa crucial em algoritmos de pesquisa, como pesquisa binária e pesquisa ternária , onde os dados precisam ser classificados antes de procurar um elemento específico.
• Gerenciamento de dados: classificar dados facilita a pesquisa, a recuperação e a análise.
• Otimização de banco de dados: Classificar dados em bancos de dados melhora o desempenho da consulta. Normalmente, mantemos os dados classificados por índice primário para que possamos fazer consultas rápidas.
• Aprendizado de máquina: a classificação é usada para preparar dados para treinamento de modelos de aprendizado de máquina.
• Análise de Dados: A classificação ajuda a identificar padrões, tendências e outliers em conjuntos de dados. Ela desempenha um papel vital na análise estatística, modelagem financeira e outros campos orientados a dados.
• Sistemas operacionais: Algoritmos de classificação são usados ​​em sistemas operacionais para tarefas como agendamento de tarefas, gerenciamento de memória e organização do sistema de arquivos.

Vantagens dos Algoritmos de Ordenação:

• Eficiência: Algoritmos de classificação ajudam a organizar dados em uma ordem específica, tornando mais fácil e rápido pesquisar, recuperar e analisar informações.
• Desempenho aprimorado: ao organizar os dados de maneira ordenada, os algoritmos podem executar operações com mais eficiência, resultando em melhor desempenho em vários aplicativos.
• Análise de dados simplificada: a classificação facilita a identificação de padrões e tendências nos dados.
• Consumo de memória reduzido: a classificação pode ajudar a reduzir o uso de memória eliminando elementos duplicados.
• Visualização de dados aprimorada: dados classificados podem ser visualizados de forma mais eficaz em tabelas e diagramas.

Desvantagens dos Algoritmos de Ordenação:

• Inserção: Se quisermos manter os dados ordenados, a operação de inserção se torna custosa, pois temos que manter a ordem ordenada. Se não tivermos que manter a ordem ordenada, podemos simplesmente inserir no final.
• Seleção de algoritmo: escolher o algoritmo de classificação mais apropriado para um determinado conjunto de dados pode ser desafiador.

Para muitos problemas, o hash funciona melhor do que a classificação, por exemplo, encontrar elementos distintos, encontrar um par com uma determinada soma.

Desafios de Algoritmos de Ordenação

Desafios de Nível Fácil

• Verifique se uma matriz está classificada
• Classificar uma matriz de dois tipos
• Classificar uma sequência de caracteres
• Classificar cada linha de uma matriz
• Classificar uma matriz
• Classificar uma lista vinculada
• Classificar em forma de onda
• Classificar por frequência
• Classificar de diferentes máquinas
• Verifique se há dois intervalos sobrepostos
• Elementos ausentes de um intervalo
• Classificar por contagem de bits definidos
• Classificar pares e ímpares colocados em ordens diferentes
• Classificando números inteiros grandes
• Classificar strings por comprimento
• Mesclar dois arrays classificados
• Classificar quando duas metades são classificadas
• 2 Soma - Par em uma matriz ordenada
• Intersecção de duas matrizes ordenadas
• União de duas matrizes ordenadas
• Salas de reunião

Desafios de Nível Médio

• Incrementos mínimos para tornar único
• Mesclar intervalos sobrepostos
• Plataformas Mínimas
• Par de elementos mais próximo
• Par de pontos mais próximo
• Problema de distribuição de chocolate
• Quantidade mínima e máxima para comprar tudo
• Particionamento de três vias
• Classificar uma matriz de 0s, 1s e 2s
• Classificar uma lista encadeada de 0s, 1s e 2s
• Contagem de inversão
• K-ésimo menor elemento
• K Menores Elementos
• 3 Soma - Encontre Qualquer
• 3 Soma - Tripleto mais próximo
• Menor diferença tripleto de três matrizes
• Mesclar K matrizes classificadas
• Mesclar K listas vinculadas classificadas
• Min Unsorted Subarray para tornar o array ordenado
• Classificar uma matriz quase classificada
• Classifique n números no intervalo de 0 a n^2 – 1
• Classificar uma matriz de 1 a n
• Classificar de acordo com a ordem definida por outro
• Intervalos máximos se sobrepõem
• Permutação com pior caso de Merge Sort
• Trocas mínimas para tornar dois arrays idênticos
• Permutar duas matrizes de modo que todos os pares de sóis sejam maiores que K
• Bucket Sort para classificar uma matriz com números negativos
• Converter um Array para a forma reduzida usando o Vector of pairs
• Verifique se a matriz pode ser classificada com troca condicional de adjacentes
• 4 Sum - Encontre qualquer (Mais problemas de 4 Sum estão na seção Difícil)

Desafios de Nível Difícil

• Mesclar sem espaço extra
• Principais K Elementos Frequentes
• 3 Soma - Trigêmeos distintos
• 4 Soma - Quádruplos Distintos
• 4 Soma - Todos os quádruplos
• 4 Soma - Quádruplo mais próximo
• Contagens de Surpasser em uma Matriz
• Contar ocorrências distintas como uma subsequência
• Subconjuntos de números consecutivos mínimos
• Trocas mínimas de Binary Tree para BST
• K-ésimo menor elemento após remover alguns inteiros de números naturais
• Diferença de frequência máxima, tal item de frequência maior também é maior
• Trocas mínimas para atingir a matriz permutada com no máximo 2 posições restantes trocas permitidas
• Tornando os elementos da matriz iguais
• Classificar uma matriz após aplicar uma equação
• Matriz de strings em ordem classificada sem copiar strings